CÁLCULO DA RAIZ QUADRADA COM APROXIMAÇÃO CENTESIMAL
Foi numa aula em junho de 1980, na Escola Municipal José Veríssimo, no bairro do Rocha, Rio de Janeiro, com o Prof. Oswaldo de Assis Gomes que aprendi esse cálculo.
Passeando na internet, encontrei alguns vídeos e publicações sobre o assunto. Percebi logo que esta geração não foi aluna do Professor Oswaldo.
A influência do Prof. Oswaldo me contagiou de tal maneira que me tornei seu colega. Sou grato a ele. Sou Professor.
A princípio, parece inútil este conhecimento, mas quando você entender e começar a acertar, vai acreditar que você é um mágico!
No final, se ousar o cálculo, faça as contas com uma calculadora.
Observe que procedimentos executados nas operações de multiplicação e divisão, que a principio causam estranhezas, mas que todos sabem fazer, acabam ajudando neste cálculo da raiz quadrada com aproximação centesimal.
A propósito, quando terminei Cálculo III, na Faculdade de Química da UFRJ, percebi que nem só de números vive a Matemática, mas de todas as "letrinhas" que desenhamos.
Boa sorte!
Como é mais de um exemplo, vou começar chamando o primeiro de primeira questão, do mesmo jeito que o Professor Oswaldo colocava em suas provas.
___
___
1ª QUESTÃO: ⎷13
a) Coloque o número 13 ao lado de uma chave matemática semelhante a da divisão. Deixe um espaço entre o numero e a chave (não deixado por mim!). Vc vai precisar para recorrer a regra de adição de zeros.
b) Escolha o número que elevado ao quadrado se aproxime do 13. No caso é o número 3.
c) Elevando ao quadrado o 3, vc encontra 9. Coloque abaixo do 13, faça a subtração. Resultado igual a 4.
d) Agora vem a regra dos zeros. Um par de zero "cai" e torna o 4, no número 400. O par é utilizado, e a cada par que vc adiciona, no final corresponderá a movimentação de uma casa numérica depois da vírgula. Aguarde. Se vc não gostou , tente dividir 216 por 2. Por favor, não vai dá 18! E sim 108.
e) Entramos agora no processo que vai tornar vc o Mágico da Matemática. Se fizer isso para os seus colegas no quadro, muitos ficarão impressionados: - Inacreditável. - Como ele conseguiu sem calculadora? - Me ensina! - Por favor.
Multiplique o número 3 por 2. No resultado 6, vc deve adicionar um espaço (veja setas!), onde colocará números idênticos, e a multiplicação formada deve resultar em um número próximo ao número 400.
f) Fazendo a multiplicação, é encontrado o valor 396. Agora são dois procedimentos: primeiro - o numero que vc usou no espaço vazio, o 6, coloque ao lado do número 3. Será o primeiro número da raiz de 13. E segundo - coloque o número 396 embaixo do 400 e faça a subtração. O que resulta em 4.
g) Desça mais dois zeros e coloque ao lado do 4, formando o número 400. Agora na raiz, vc tem o número 36. Multiplique por 2. E com o resultado, 72, vc vai de novo adicionar um espaço (veja setas!), onde colocará números idênticos, e esta multiplicação formada deve resultar em um número próximo ao número 400. Observe que colocando o número 1, isso não será possível. Se fizer, o resultado fica 721 x 1 = 721, ou seja, maior que 400. Então não pode. Ultrapassou. Neste caso escolha o número zero.
Multiplique 720 x 0 = 000. Subtraia de 400, o que resulta em 400
h) Nesse momento o número Zero ocupa o lugar na raiz, depois do número 6 (veja seta!). Pronto. Acabou. Ou quase!
i) Cada dois zeros "caídos" correspondem a um "pulo" de duas casas numéricas. Veja o número 400 (o resto da conta). Como foram 2 vezes a descida de dois zeros, isso corresponderá a 2 "pulos", englobando quatro casas numéricas. Sendo o resto 0,04. Considerando que foram 2 operações de descidas dos zeros, no número 360, movimente a vírgula 2 casas numéricas a partir da direita. Portanto, a raiz é 3,60.
Não acredita? Use a sua calculadora.
___
2ª QUESTÃO: ⎷9,135
Calcule a raiz quadrada de 9,135 com aproximação centesimal.
Seguiremos os mesmos passos já descritos. Tão somente agora, trata-se de um número decimal.
Veja:
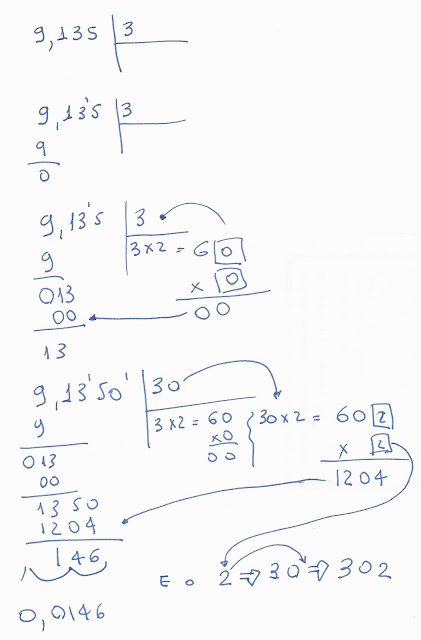
Cada dois números "caídos" correspondem a um "pulo" de duas casas numéricas. Veja o número 146 (o resto). Como foram 2 vezes, primeiro o 13 e depois o número 50 (observe que foi acrescentado um zero ao lado do número 5), isso corresponde a 2 "pulos" de duas casas, a partir da direita, englobando quatro casas numéricas. Sendo, portanto, o resto 0,0146 (veja figura). Também como foram 2 operações de descidas, no número 302, movimente a vírgula 2 casas numéricas a partir da direita. Logo, a raiz é 3,02.
Resposta: 3,02 com resto 0,0146.
Prezado amigo ou amiga, se for usar, cite o endereço do blog profmarcelomoreno2010.
Precisamos de FAIRPLAY também na Academia.
Obrigado meu querido Prof Oswaldo de Assis Gomes.
Conversei com ele hoje, 27/05/2021, ainda em atividade profissional com seus 91 anos.
Paz.








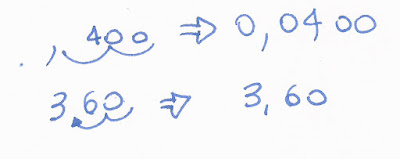






Comentários